The Rhythmic Series: an expansion of musical possibilities.
Could Pythagoras's ancient ideas build a rhythmic map for modern music?
About 2500 years ago, the Greek philosopher Pythagoras drew a link between matter, mathematics, and music. Through a series of experiments with sound, he discovered a harmonious world of tonality that joined the cerebral world of mathematics to the physical laws of the universe.
By experimenting with weights, lengths, and proportions of various materials — such as the plucking of strings divided in simple mathematical ratios — he discovered the harmonic series. This series is an infinite sequence of musical tones (or harmonics) that are mathematically related to a fundamental frequency. Essentially, it is a formula for understanding the relations between musical tones.
If Pythagoras and the harmonic series seem irrelevant today, think again. The harmonic series provides a deep insight into music, with many of the questions Pythagoras raised in the ancient world still debated today. However, one aspect of his theory remains largely unexplored: Could his ideas about harmony apply to the temporal organisations of sounds? In other words, could the formula of the harmonic series be applied to rhythm?
What exactly is the Harmonic Series?
The harmonic series is a beautiful but often neglected concept, which is a shame, because its simple elegance can deepen one’s relationship to music and provide a context for the origin of certain musical ideas.
At its heart, the harmonic series is a formula — a kind of ancient musical algorithm — which can be understood most viscerally by following some of the methods Pythagoras used to explore it.
If you divide a taut string in half and pluck it, it will produce a higher-pitched note than if the string is plucked undivided. Most significantly, the new note will sound in tune with the original undivided string’s note. The distance between these notes, represented physically on the string and experienced psychologically through the perception of the notes, is called an interval. In the case of our imagined string, the interval is an octave, the most fundamental of intervals.
The process of dividing the string by whole-number ratios can be continued indefinitely. If the string is divided by one third and plucked, an even higher note is produced, an octave + fifth — a quintessential interval in music. One can then continue to divide the string by a quarter, fifth, sixth and so on, each of which produces a unique musical interval.
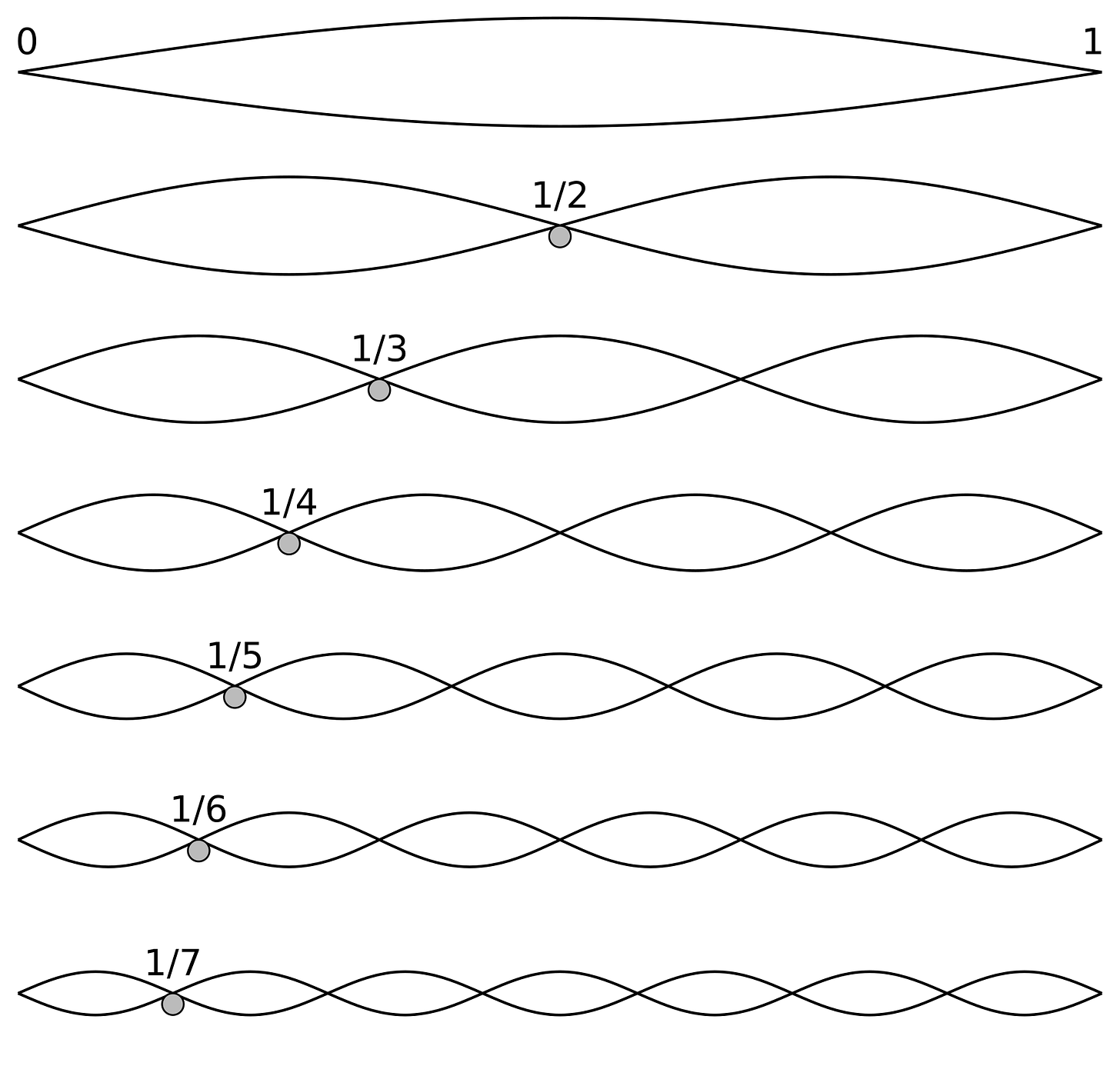
Through this process, Pythagoras revealed notes within notes, referred to as harmonics, or overtones. The mathematical relationships that define these intervals provide tools for constructing harmony — the art of playing multiple notes simultaneously. Remarkably, the first four harmonics in the harmonic series contain all the intervals needed to create a major chord; the primary building block for chordal harmony. One way to summarise this is that within the microcosm of a vibrating string lies the potential for an orchestra.
This diagram helps visualise the different harmonics and the mathematical points at which Pythagoras held down each string. The top string is called the fundamental and produces the lowest pitch note; each subsequent string represents a higher-pitched harmonic that relates to the fundamental.
To gain a deeper understanding of harmonics, it helps to look at sine waves, which are the simplest possible sounds in the universe — so simple that they can only be generated electronically.
The sine wave looks like a wave in the ocean, which is appropriate, as sound travels by waves. The frequency of the waves determines the pitch of the note, with shorter waves representing higher notes; the height of the wave determines its loudness.
This image shows two simultaneous sound waves. The blue wave is called the fundamental and is always the lowest-pitched note in the series (if an undivided string is plucked, we hear the fundamental). The red wave is called a harmonic because it is harmonically related to the fundamental, which is to say, it is mathematically related. In this case, it is double the frequency of the fundamental.
This shows the first six harmonics.
The continual division of the fundamental tone results in the harmonic series, an aesthetically and intellectually beautiful pattern.
What would the Rhythmic Series look like?
Pythagoras’s theories and experiments explored harmony, the celebrated art of combining sounds concordantly. Harmony can be thought of as a vertical musical dimension, wherein notes are meticulously stacked on top of each other, and are called chords. Successfully building chords requires an understanding of certain musical intervals within the harmonic series.
A harmony-centred perspective of music is cultural, as what is considered significant in music varies across traditions. Chordal harmony is demonstrably not the quintessence of music, since there are entire musical traditions that do not use chords at all, such as the Indian classical music tradition, which is constructed using ragas, talas, and microtonal gamakas, but not chordal harmony.
The formula that Pythagoras discovered could equally be applied to the temporal or horizontal organisation of sound, rhythm. Had Pythagoras done so, ancient music might have contained a rhythmic series in addition to the harmonic series, and music may have sounded and evolved quite differently.
So, let’s attempt to create a rhythmic series.
This shape can act as the starting point for exploring the idea of a rhythmic series. Unlike the wave with its up and down motion, this shape only has the upper motion. It creates a dome that symbolises a container of time, whose peak represents the halfway point of its duration.
This image shows the simplest polyrhythm, 1:2. The blue dome covers the full horizontal, while the two red domes divide the horizontal space evenly.
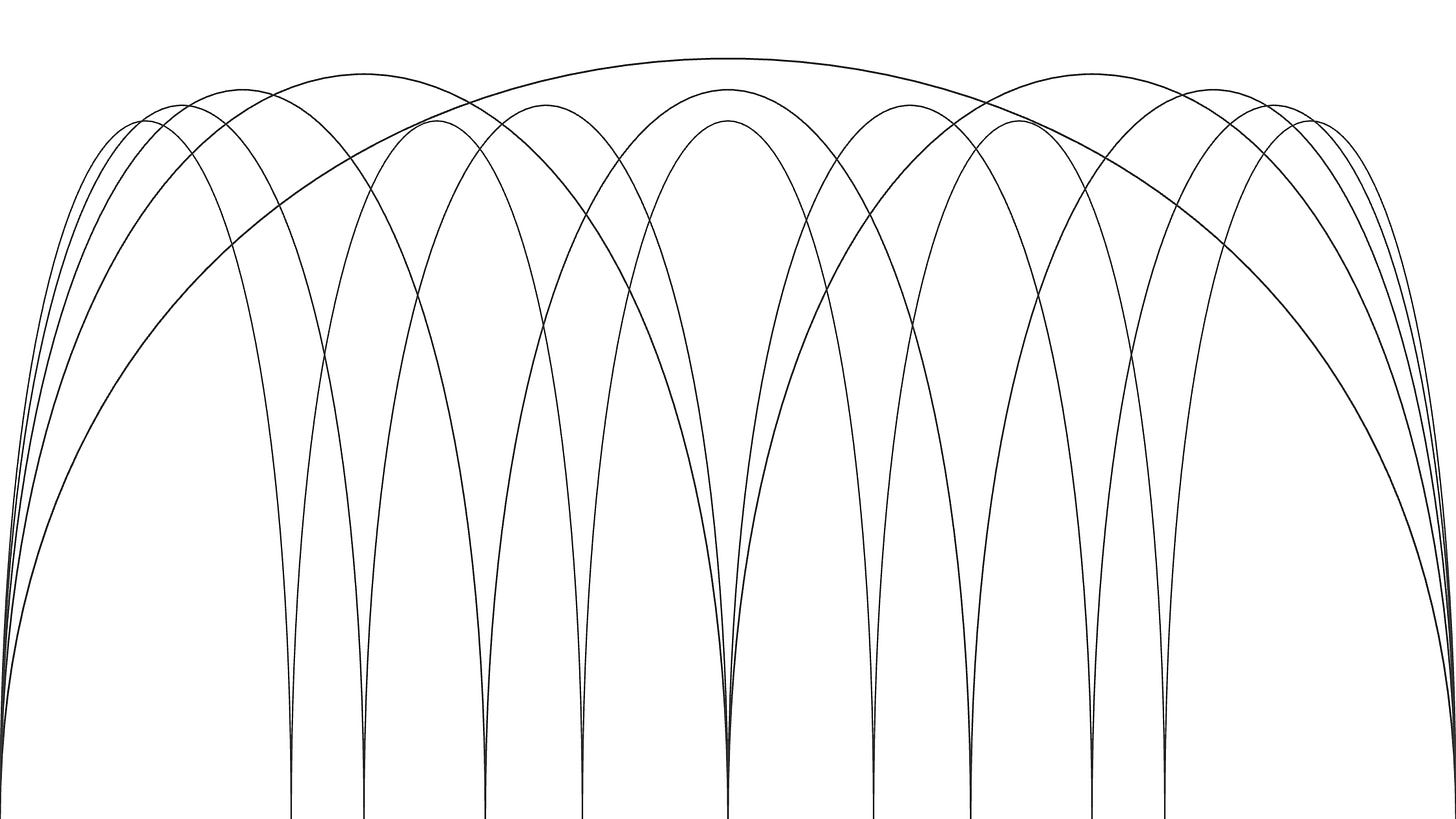
The complexity rapidly increases with three layers, 1:2:3. A division of one, two, and three.
A significant increase in complexity with five layers, 1:2:3:4:5. For aesthetic reasons, as the number of divisions increases, the height of the domes has been lowered.
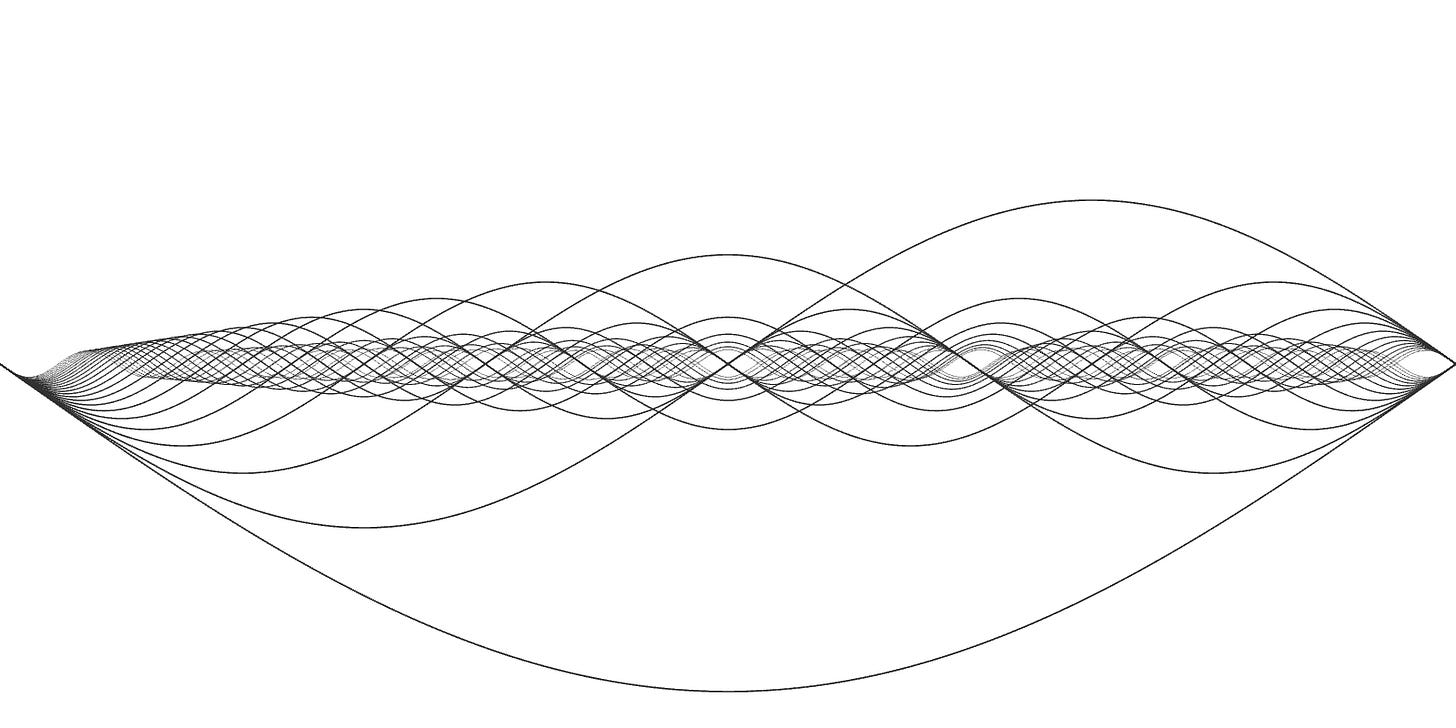
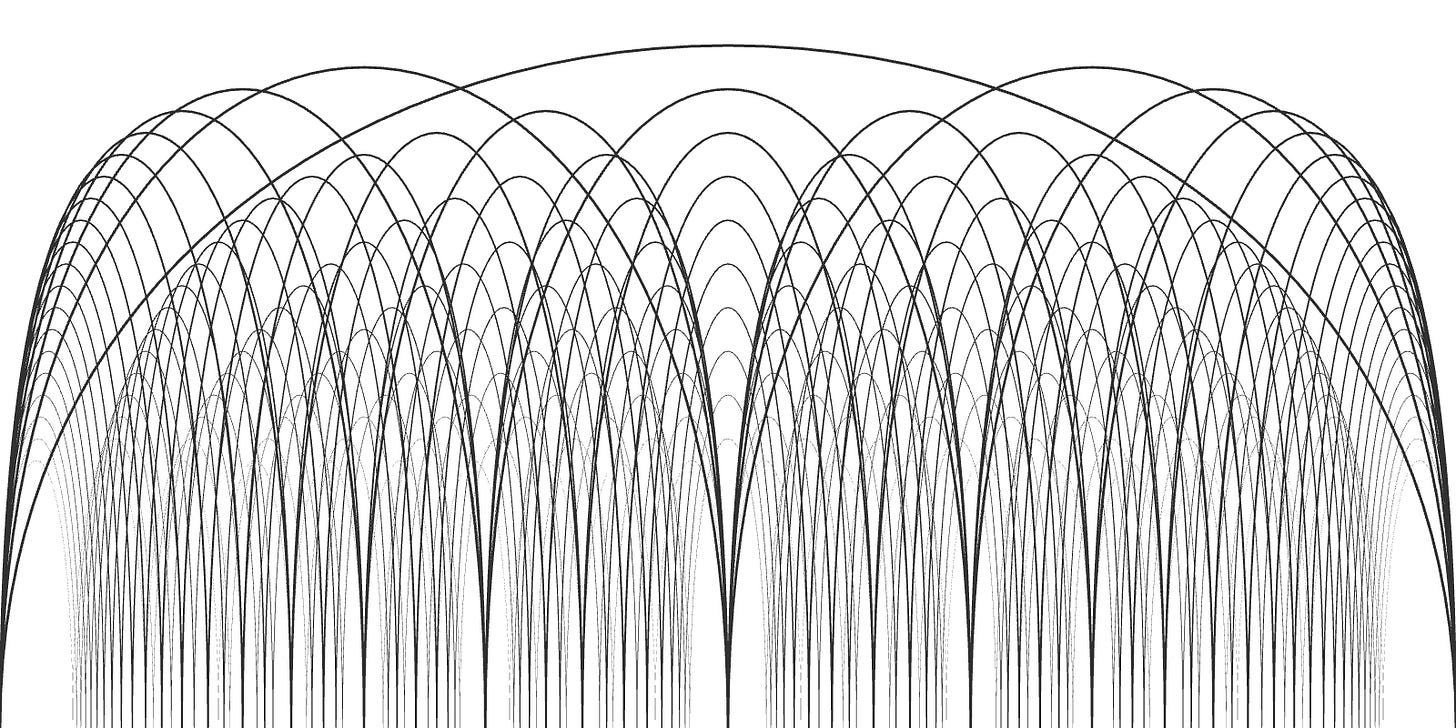
Twenty layers of curves create a self-similar fractal. The rhythmic series.
Besides the attractive aesthetic quality, I find the points of convergence along the bottom of the image insightful. Their convergences represent rhythms within rhythms, or structures within structures. A rhythmic series could help in the development of rhythmic theory by providing a visual, musical, and mathematical map of time.
When Pythagoras discovered the harmonic series, he did so within the biases of his culture and its limits of knowledge. We now know that what divides rhythms from pitches is only the speed at which they vibrate: slow down a note sufficiently, and it becomes a rhythm; speed up a rhythm sufficiently, and it becomes a note.
For those of us raised in the Western musical tradition, the highly sophisticated rhythmic concepts of traditions such as Indian classical music can act as a reminder of the shortcomings of Western rhythmic theory. Yet within the Western tradition exists an emerging tool that could help develop this temporal aspect of music, the rhythmic series. More than two thousand years after Pythagoras lived, we can return to his ideas and build upon them, to extend our understanding of time, music, and the universe.











The usual excellent writing on music theory! And whilst on the subject of Ancient Greek dudes can we hope for an essay on Euclidean Rhythms?
Fantastic! But it seems like the audio files are all the same sine wave, when I think you intended for each one to demonstrate a different example?